Изучение структурных средних и показателей вариации

Цель работы: Изучить моду и медиану, показатели признака вариации в ряду (среднее квадратическое отклонение, линейное отклонение, дисперсия, коэффициент вариации), решить практические задачи.

Краткие теоретические сведения

Мода - значение признака, наиболее часто встречающееся в изучаемой совокупности. Для дискретных рядов распределения модой является вариант с наибольшей частотой.

Для интервальных вариационных рядов распределения мода рассчитывается по формуле:

Где M0 - мода;

xM0 - нижняя граница модального интервала;

iM0 - величина модального интервала;

fM0 - частота модального интервала;

fM0-1 - частота интервала, предшествующего модальному;

fM0+1 - частота интервала, следующего за модальным.

Медианой называется величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В ранжированном ряду из отчетного числа членов медианой будет средняя арифметическая из двух вариантов, расположенных в средине ряда.

Медиана дискретного вариационного ряда определяется по сумме накопленных частот, которая должна превышать всего объема единиц совокупности. Для интервальных вариационных рядов медиана может рассчитываться по формуле:

Где Me - медиана;

xMe- нижняя граница медианного интервала;

iMe - величина медианного интервала;

- сумма частот ряда;

SMe-1 - сумма накопленных частот ряда, предшествующих медианному интервалу;

fMe - частота медианного интервала.

Задача 4.18

По данным выборочного обследования получены данные о распределении семей по числу детей:

Определите для каждого района:

1) среднее число детей в семье;

2) моду и медиану.

Решение:

1)

Определим в каждом районе среднее число детей в семье, используя формулу средней взвешенной:

I район

район

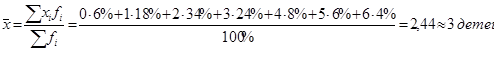
район

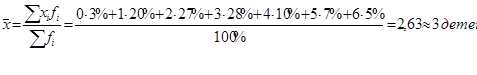
2)

Определим для каждого района моду и медиану:

I район

Так как, мода - это наиболее часто встречающееся в изучаемой совокупности значение признака, то в нашей совокупности часто встречается число детей равной 1. Следовательно, мода равна 1.

M0=1 ребенок

Для нахождения медианы:

а) проранжируем ряд: 4; 5; 8; 13; 20; 22; 28

б) найдем номер медианы

в) Me=13% - 4 детей

II район

M0=2 детей

Найдем медиану:

а) 4; 6; 6; 8; 18; 24; 34

б) найдем номер медианы

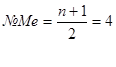
в) Me=8% - 4 детей

III район

M0=3 детей

Найдем медиану:

а) 3; 5; 7; 10; 20; 27; 28

б) найдем номер медианы

в) Me=10% - 4 детей

вариация отклонение интервал медиана

Еще статьи по экономике

Имущество предприятия общественного питания
В современных экономических условиях деятельность каждого хозяйственного субъекта является предметом внимания обширного круга участников рыночных отношений, заинтересованных в ...

Учет и анализ движения денежных средств на примере ООО Охранное предприятие Азимут
Среди главных проблем российской экономики многие экономисты выделяют дефицит денежных средств на предприятиях для осуществления ими своей текущей и инвестиционной деятельност ...

Исследование в экономике теории магистралей
В экономической теории на первоначальном этапе ее развития редко использовались математические формулировки. Тем не менее, многие классические доктрины экономики в словесной, ...